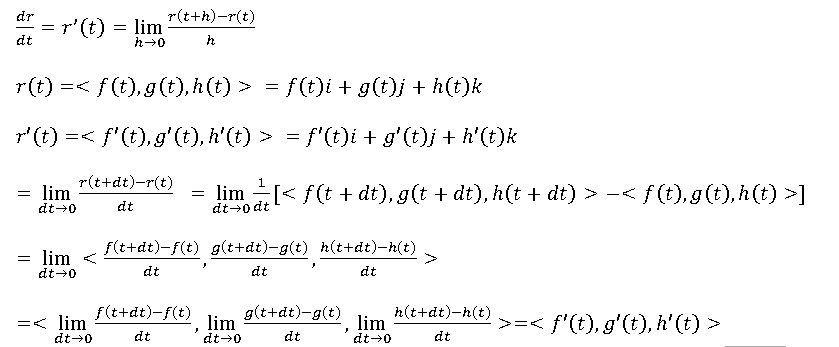상위문서 : 미적분학
필수참고문서 : 벡터, 외적, 내적
목차
1. 개요
2. 벡터함수의 극한
3. 벡터함수의 미적분
4. 호의 길이와 곡률벡터
1.개요
벡터함수는 정의역이 실수의 집합이고, 치역이 벡터의 집합인 함수이다. 예를 들어 벡터함수 r(t)을 r(t)= <f(t), g(t), h(t)>로 정의하면 어떤 실수 t를 유클리드 3차원 공간의 벡터로 나타내는 벡터함수로 여기서 벡터의 각 성분의 함수는 r의 성분함수(component function)라 하는 실수값 함수이다. 이것을 다음과 같이 쓸 수 있다.
r(t)=<f(t), g(t), h(t)> = f(t) i + g(t) j + h(t) k
이 벡터 함수를 그래프로도 나타낼 수 있는데 벡터 함수의 각 성분을 x,y,z에 대응해보면 다음과 같다. x=f(t), y=g(t), z=h(t)
다음은 벡터함수 r(t)=<t-2sin(t), t^2> 함수를 그려본 것이다. 원래는 3차원 벡터함수를 그릴려고 했는데 울프램 알파 웹버전에서는 2차원밖에 지원을 안해준다.
r(t)=<f(t), g(t), h(t)> = f(t) i + g(t) j + h(t) k
이 벡터 함수를 그래프로도 나타낼 수 있는데 벡터 함수의 각 성분을 x,y,z에 대응해보면 다음과 같다. x=f(t), y=g(t), z=h(t)
다음은 벡터함수 r(t)=<t-2sin(t), t^2> 함수를 그려본 것이다. 원래는 3차원 벡터함수를 그릴려고 했는데 울프램 알파 웹버전에서는 2차원밖에 지원을 안해준다.
2.벡터함수의 극한
이 벡터 함수에서의 극한은 각 성분함수에 극한을 취한것과 같다.
즉 벡터함수 r이 a에서 연속이기 위한 필요충분조건은 그의 성분함수 f, g, h가 a에서 연속인 경우이다.
3.벡터함수의 미적분
벡터함수의 극한은 벡터함수에 있는 성분함수에 대한 것이였다. 더 나아가 벡터 함수의 미분은 각각의 성분함수를 매계변수에 대해 미분을 취한 것과 같다.
위 미분에 따라서 실수 함수의 법칙이 벡터함수에 대해서도 가지고 있음을 보여준다. 다음은 벡터함수의 미분 법칙이다.
위 법칙에서 실수 함수에서 없었던 4와 5 즉 내적과 외적에 대하여 미분법칙이 성립하는지만 증명해보도록 하자.
- 내적에 대하여
- 외적에 대하여
벡터함수의 정적분은 미분과 마찬가지로 각각의 성분함수에 대해 정적분을 한 것과 같다.
벡터함수의 부정적분은 일반적인 부정적분과 마찬가지로 적분상수가 생긴다.
4.호의 길이와 곡률벡터
예전 선적분을 했을 때를 생각해보자
지금까지 벡터함수를 보면 엄청나게 휘어져 있는 아크로바틱한 곡선들을 보았다. 그러면 이 곡선의 휘어져 있는 정도를 수치로 나타낼 수 있지도 않을까?
